Given an array of integers, find all the sub array combinations (without ordering).
For example,
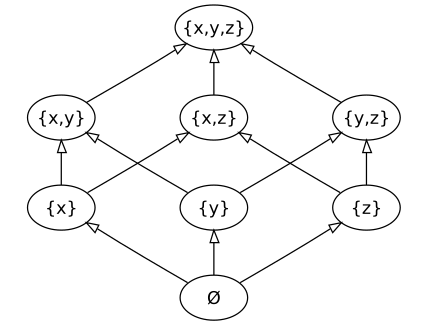
Given (x, y, z) – result should be (x), (y), (z), (x, y), (x, z), (y, z), (x, y, z) – see picture above
Given (0, 1) – result should be (0), (1), (0, 1)
Given (0, 1, 2, 3) – result should be (0), (0, 1), (0, 1, 2), (0, 1, 2, 3), (0, 1, 3), (0, 2), (0, 2, 3), (0, 3), (1), (1, 2), (1, 2, 3), (1, 3), (2), (2, 3), (3)
Here is the design for the recursion:
Consider input array (0, 1) – the output (), (0), (1), (0, 1) matches (00, 01, 10, 11)
()=(00) – both bits are off, therefor both input items are excluded
(0)=(01) – only first bit is set, therefor only first input is included
(1)=(10) – only second bit is set, therefor only second input is included
(0, 1)=(11) – both bits are set, therefor both inputs are included
Got it?
Another one:
Consider input array (0, 3, 6) – the output (), (0), (3), (0, 3), (6), (6, 0), (6, 3), (0, 3, 6) matches (000, 001, 010, 011, 100, 101, 110, 111)
We will use it in our binary solution!
Here are the steps:

Final result is (0), (1), (0, 1) !

For example,
Given (x, y, z) – result should be (x), (y), (z), (x, y), (x, z), (y, z), (x, y, z) – see picture above
Given (0, 1) – result should be (0), (1), (0, 1)
Given (0, 1, 2, 3) – result should be (0), (0, 1), (0, 1, 2), (0, 1, 2, 3), (0, 1, 3), (0, 2), (0, 2, 3), (0, 3), (1), (1, 2), (1, 2, 3), (1, 3), (2), (2, 3), (3)
Approach (Recursive)
Notice that for the first item ‘0’, we have 7 subarrays that start with ‘0’, where every subarray builds on one of the previous. For the second item ‘1’, there are less sub arrays, For the last item ‘3’, there are no subarrays.Here is the design for the recursion:
- Create a new empty integer array called source, call calculatePowerSetRecursive
- Iterate on the input from index 0
- For each item:
- Add the item to the source array, clone the the source array
- Add the source array to the result
- Call calculatePowerSetRecursive with the new source array, and increate the starting index, such that the iteration start from the next item
- Our stopping point (base case) is where the starting index is as big as the length of the array.
Approach (Binary representation)
If you look closely at the results, you will notice that output is actually the binary combinations of the input .Consider input array (0, 1) – the output (), (0), (1), (0, 1) matches (00, 01, 10, 11)
()=(00) – both bits are off, therefor both input items are excluded
(0)=(01) – only first bit is set, therefor only first input is included
(1)=(10) – only second bit is set, therefor only second input is included
(0, 1)=(11) – both bits are set, therefor both inputs are included
Got it?
Another one:
Consider input array (0, 3, 6) – the output (), (0), (3), (0, 3), (6), (6, 0), (6, 3), (0, 3, 6) matches (000, 001, 010, 011, 100, 101, 110, 111)
We will use it in our binary solution!
Here are the steps:
- Iterate on all the numbers from 1 or 2^Array.Length (2^2 = 4) exclusive.
- For each iteration (from 1..3)
- Create new integer array
- Convert the iterator index to binary mask (1 becomes 01, 2 becomes 10, 3 becomes 11).
- Iterate on the items in the input array (0, 1).
- If the bit (of the binary mask ) in the item index location is set: add the item to the integer array.
- Add the integer array to the result!

Final result is (0), (1), (0, 1) !
Tests
public class PowerSetCalculatorTest {
private static final Boolean USE_BINARY = true;
@Test
public void calculatePowerSet_threeItems() throws Exception {
final PowerSetCalculator calculator = createCalculator();
final List<List<Integer>> result = calculator.calculatePowerSet(new int[]{0, 1, 2});
printResult(result);
List<int[]> expected = new ArrayList<>();
expected.add(new int[]{0});
expected.add(new int[]{0, 1});
expected.add(new int[]{0, 1, 2});
expected.add(new int[]{0, 2});
expected.add(new int[]{1});
expected.add(new int[]{1, 2});
expected.add(new int[]{2});
assertEquals(expected.size(), result.size());
compareArrays(expected, result);
}
@Test
public void calculatePowerSet_twoItems() throws Exception {
final PowerSetCalculator calculator = createCalculator();
final List<List<Integer>> result = calculator.calculatePowerSet(new int[]{0, 1});
printResult(result);
List<int[]> expected = new ArrayList<>();
expected.add(new int[]{0});
expected.add(new int[]{0, 1});
expected.add(new int[]{1});
assertEquals(expected.size(), result.size());
compareArrays(expected, result);
}
private void printResult(List<List<Integer>> lists) {
for (List<Integer> result: lists ){
for (Integer item: result) {
System.out.print(item + ",");
}
System.out.println();
}
}
private PowerSetCalculator createCalculator() {
if (USE_BINARY) {
return new PowerSetCalculatorBinary();
}
return new PowerSetCalculatorRecursive();
}
private void compareArrays(List<int[]> expected, List<List<Integer>> result) {
Boolean[] valid = new Boolean[result.size()];
for (int[] expArray : expected) {
for (int i = 0; i < result.size(); i++) {
List<Integer> res = result.get(i);
final int[] resArray = getArray(res);
if (Arrays.equals(expArray, resArray)) {
valid[i] = true;
continue;
}
}
}
for (int i = 0; i < valid.length; i++) {
assertEquals("No match at index " + i, true, valid[i]);
}
}
private static int[] getArray(List<Integer> buffer) {
final int[] array = buffer.stream().mapToInt(j -> j).toArray();
return array;
}
}
Solution (recursive)
public class PowerSetCalculatorRecursive implements PowerSetCalculator{
@Override
public List<List<Integer>> calculatePowerSet(int[] set) {
List<List<Integer>> result = new ArrayList<>();
calculatePowerSetRecursive(set, 0, result, new ArrayList<Integer>());
return result;
}
private void calculatePowerSetRecursive(
int[] set,
int index,
List<List<Integer>> result,
ArrayList<Integer> buffer) {
for (int i = index; i < set.length; i++) {
ArrayList<Integer> newBuffer = new ArrayList<>(buffer);
newBuffer.add(set[i]);
// Add buffer to result
result.add(newBuffer);
// Call recursion with next index and updated buffer
calculatePowerSetRecursive(set, i+1, result, newBuffer);
}
}
}
Solution (Binary)
public class PowerSetCalculatorBinary implements PowerSetCalculator {
@Override
public List<List<Integer>> calculatePowerSet(int[] set) {
List<List<Integer>> result = new ArrayList<>();
int numberOfCombinations = (int) Math.pow(2, set.length);
for (int mask = 1; mask < numberOfCombinations; mask++) {
List<Integer> sequence = getSequence(mask, set);
result.add(sequence);
}
return result;
}
private List<Integer> getSequence(int mask, int[] set) {
List<Integer> result = new ArrayList<>();
for (int index = 0; index < set.length; index++) {
int factor = 1 << index;
if ((factor & mask) > 0){
result.add(set[index]);
}
}
return result;
}
}
Comments
Post a Comment